What is bloom filter?

A bloom filter is a probabilistic data structure that is used to test if an element has been seen before. A simple implementation for checking the presence of an element would likely just use a set.

Let’s consider a scenario where we want to check if it is a visitor’s first time coming to our website.

type VisitorTracker struct {
	visitors map[string]struct{}
}

func NewVisitorTracker() *VisitorTracker {
	return &VisitorTracker{
		visitors: make(map[string]struct{}),
	}
}

func (vt *VisitorTracker) AddVisitor(userID string) {
	vt.visitors[userID] = struct{}{}
}

// HasVisitedBefore returns true if the user has visited before
func (vt *VisitorTracker) HasVisitedBefore(userID string) bool {
	_, ok := vt.visitors[userID]
	return ok
}

func main() {
	vt := NewVisitorTracker()
	vt.AddVisitor("user_1")
	vt.AddVisitor("user_2")
	vt.AddVisitor("user_3")

	fmt.Println(vt.HasVisitedBefore("user_1")) // true
	fmt.Println(vt.HasVisitedBefore("user_4")) // false
}

This code is just a simple wrapper around a set. This works fine for simple cases, but what happens if we start to get a lot of visitors? The underlying set must remember all of the user IDs that we’ve seen so far. This means that our space usage will grow linearly with the popularity of our website.

In technical term, the space complexity of this solution is O(n) where n is the number of visitors, thus the space complexity is linear.

This is where bloom filters shine. Usually, we don’t care about 100% accuracy when dealing with these types of problems. Does it matter if we don’t show that special banner to every single new user? Probably not. Bloom filters allow us to exploit this lax requirement and put a cap on our memory usage in exchange for the occasional false positive.

Bloom filters work by operating on an underlying bit array. The bloom filter will have some number of hash functions that take in a value and produce an index somewhere within the bit array. Usually, the bit arrays are much larger, but we’ll walk through a simple example with a size 20.

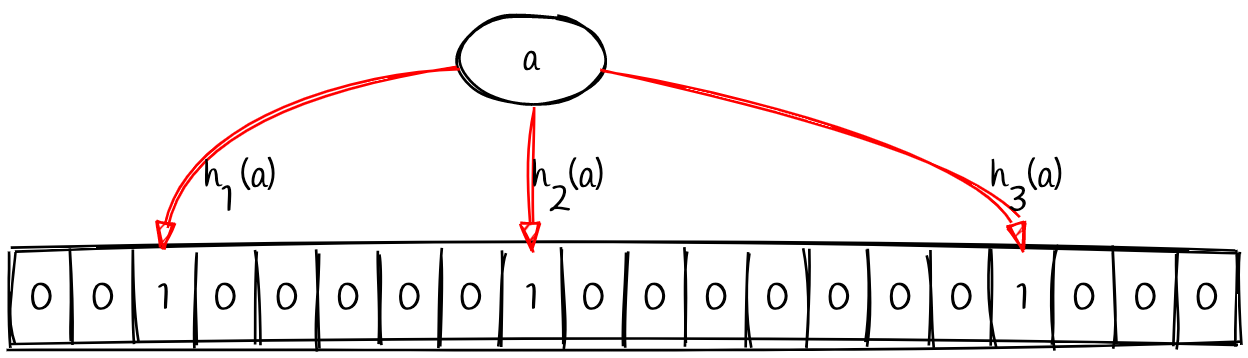
Now let’s say our bloom filter uses three hash functions (h1, h2, and h3). Passing in the value a to each of these functions will produce three different indexes within our bit array. Inserting the values means that we will flip the bits at these three indexes to 1.

Let’s add a couple of other values (b and c) to our bloom filter to see what the bit array might look like.

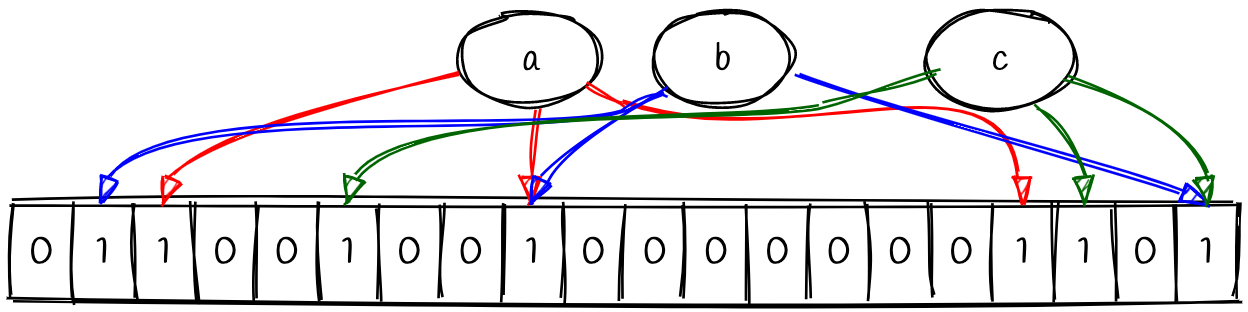
Notice that we’ve got some collisions. Values a and b have a collision in the middle and value b and c have a collision on the right. This is okay. This is where part of the probabilistic nature of the bloom filter comes in. We’ll come back to this.

So how do we check for the presence of a value? Well, our hash functions are deterministic, so they will always yield the same indexes if we hash the value again. Let’s check our Bloom Filter for two values b and d.

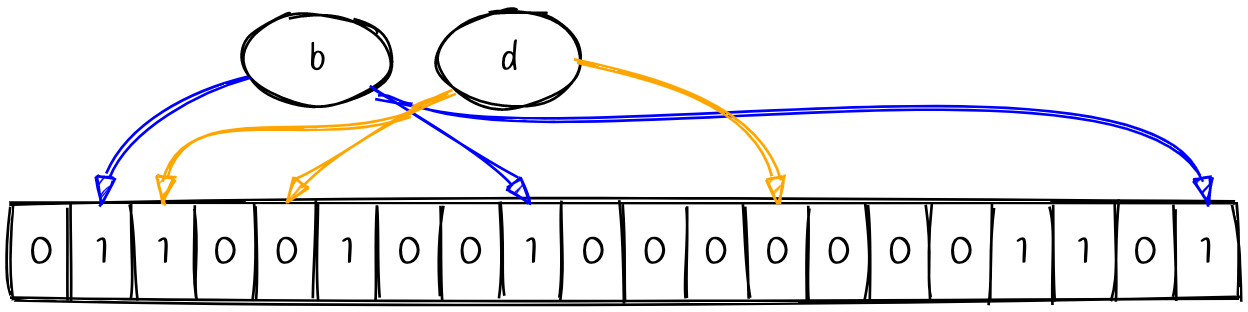
The indexes for d point to two bits that are not turned on. Since we’ve encountered some bits that are not flipped, then we can be confident that d has not been seen before. All of the indexes for the value b have bits that are flipped on. This means that the value has probably been seen before.

Let’s look at another example to understand why we can’t be 100% certain that the value has been seen before. Consider a new value, e.

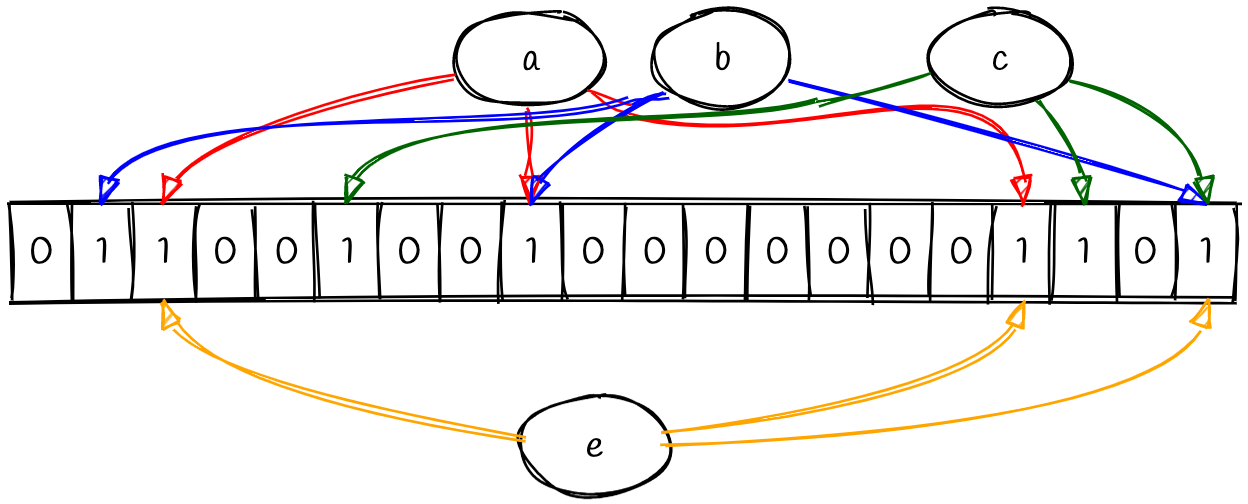
We never inserted the value e, but all of the hash functions lead us to bits that are flipped on. This is because all three indexes collide with other values that we’ve inserted. This shows us how false positives are possible and why we can only say that entries are probably present when performing a check. Conversely, a bloom filter will never produce a false negative. Again, this is because all of our hash functions are deterministic. If we’ve seen a value before then, we can be certain that all of its bits will be flipped.

Usually, collisions are much less likely than we’ve seen in the examples above since much larger bit arrays are used. Bloom filter implementations typically allow the user to choose the size of the bit array and the number of hash functions. This allows the developer to trade space for accuracy.

References

• https://yetanotherdevblog.com/bloom-filters/